Till we meet in hell race report

The 4th annual TMR end-of-the-season race was held at Thorncrag bird sanctuary and directed by Val, who marked out a sweet 1.4 mi loop with four segments:

1) steep climb on easily runnable singletrack

2) a technicalish singletrack descent

3) a longer climb with a couple very small walls that were run only because they were short

4) a fun, extremely fast run-out on wide doubletrack

I enjoyed the conversation on the first lap with David Roberts but he tired of my conversation or pace and passed me, which ignited my mojo and reminded me that we were racing. Other than lap one, my pacing was surprisingly even. I misread my watch on the final descent and turned up the gear knob to 11 so as to finish the lap before the 1:30:00 time limit, but then was told by all the runners pooled at the bottom/start that I still had 0:03:30 left. Ouch. I struggled through .3 miles of steep climbing.

Following the race all the TMs partook in some hearty drinking, eating, and awarding. I won some barefoot champagne for my racing efforts (Thanks Val!) and was voted biggest geek by my peers. Next post I will put something up worthy of that award!

Splits (each lap ~ 1.4 mi)

1      11:42

2      10:40

3      10:41

4      10:36

5  10:40

6      10:38

7      10:49

8      10:46

0.3mi   03:13.3

Bond Brook 10 mi trail race

Bond Brook is the new set of xc ski trails and singletrack mt. bike trails in Augusta. Overlay the east side of Bradbury on top of Pineland and multiply the elevation by 1.5 and voila! Bond Brook. This race was not on my radar until yesterday when I opted out of Mayor's Cup 5K for something closer. I'm not sure why as my weekly mileage is now half of what it was this summer and I haven't run more than 9 miles in one run in over 6 weeks. Moving from a flat 5K to 10 miles of extremely undulating terrain was probably an unwise decision.

The course is two loops of repeated alternating between wide ski trails and narrow single track. The ski trails were a roller coaster - there was rarely any length of something flattish. It was bone-jarring descents or lung-bursting climbs. Like Pineland, most of these were short-lived but some of each were quite extended. By contrast the singletrack seemed flattish, like the east side of Bradbury, but I think that was an illusion as the map shows these too had large (usually) ascents, it just took lots of tight twisty turns to complete the climb.  The singletrack was in sweet shape. I had both my nike spikes and my Inov8 195s and unwisely chose the 195s. The last mile of singletrack had lots of slimey turns on a cambered trail bed and it took some tip toeing to not slide down.

Some stats:

Bond Brook 10 mile: Garmin 305 reads: 9.46 mi, 1739' elevation = 183 feet/mi

Pineland 25K: Garmin 305 reads: 15.3 mi, 1772' elevation = 116 feet/mi

Bradbury Breaker: Garmin 305 reads 8.78 mi, 1537' elevation = 175 feet/mi

None of the climbs are as steep as the Breaker but there is very little flat.

My race:

I actually felt pretty good given that I lost my running mojo sometime in August. The first 2 miles of my 2nd loop was noticeably slower but I was slowly reeling in a young guy in front. On a long descent during the 3rd mile of loop 2 I nearly caught him and there was a short flat section before turning off the ski trail and onto the slimey mile of singletrack. I decided this was my move and I accelerated and just beat him to the trail. He hung onto me for maybe 0.5-0.75 miles which pushed me some but then he fell back when the singletrack started to climb. Had I not made my earlier move I probably would have been complacent to just sit behind him on the singletrack and run his pace. As a result of passing him, the 4th mile of loop 2 was only slightly slower than in loop 1 and my last mile of loop 2 was nearly 30s faster. So all in all I had about a 34s positive split, which doesn't seem too bad given no prior knowledge of the course

Mile Loop1 Loop2 Diff

1      7:24     7:52    +28

2      7:23     7:43    +20

3      7:46     8:00    +14

4      8:24     8:30    +6

5      5:57     5:23    -34

___________________

     36:54     37:28    +34

I think I came in 5th place, 2-4 minutes behind 1-4, and 1st master. Unfortunately I googled places 1-4 and noticed that I beat them all in summer road races so not sure what this says about my current fitness. I Want to do the NE XC in two weeks. The positive is, Franklin Park is a fast course and only 5 miles. The negative is my fitness is plummeting precipitously.

Tapers and Cognitive Biases

Back in the spring, I asked Kevin Tilton about tapers and specifically mentioned Jim Johnson who races every weekend and I wondered what he could do if he, you know, tapered. Kevin thought tapers were overrated and mentioned that his best races were with little to no taper. I had heard this before from posters on the famous LRC message board but had discounted it as anecdotal evidence (which it is). I haven't really researched the ex phys literature but I do recall that Rob Sleamaker briefly reviewed evidence from the literature that claims a proper taper increases performance by 1-3% or something like that. I was thinking about this recently because of two races this year compared to last year. Compared to this year, I ran a faster pace at the Bradbury Breaker and the Craig Cup last year despite having run the Beach to Beacon the day before the Breaker and the Maine Marathon 6 days before the Craig Cup. This year I was fresh for both (The B2B was 8 days earlier and I ran no marathon this year). I am now questioning the value of tapers. It's these sort of experiences that are very powerful in forming/re-inforcing (probably erroneous) beliefs that contradict conclusions based on more reliable evidence (i.e. science).

2nd Thoughts on cross training

Ass hurts. Going out for a roller ski. Running downhill fast sucks.

Deep Waste of Time

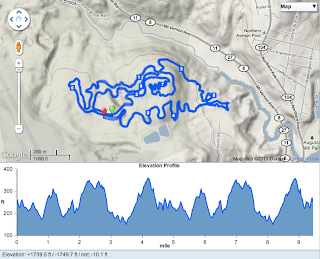
This post is about solitaire, but it's related to my work so a little background on what I do. I'm essentially a computational biologist, that is, I study biological problems using computational methods. Computational methods are used when either 1) the scientist doesn't know math well enough to solve a problem analytically, or 2) the problem is too difficult or too long to solve analytically. Both apply to me. The major computational method that I use is simulation and I typically use a simulation to solve optimization problems. So for example, I might be interested in the optimal motion of a fruit fly wing to balance weight and maximize thrust (forward flight force). There's lots of parameters that can go into a computer model such as the wing beat frequency, and the wing beat amplitude, and how much the wing rotates during the down or upstroke, and how rapidly it rotates, etc. etc. A simulation is used to explore combinations of the different values that a parameter may take. An exhaustive search (I don't know the technical term) would just try all combinations throughout the range of values for each parameter. This can be computationally intensive and most of the solutions will be pretty dumb but if the model itself is simple (computationally quick) then a large parameter space can be searched in a short time. If the model is computationally slow then it's better to use some kind of smart strategy to search only part of the parameter space (the range of parameter values).

Still with me? One smart way to search a subset of the parameter space is to use evolutionary or genetic algorithms. I don't do these and really know little about them but essentially a population/evolution approach is used where random variation is added to the parameters in a population of "strategies" and the strategy that has the highest performance (thrust in the case of my fly wing) is selected and then mutated (that is copied and the random values are added to the parameters) and etc. etc until the strategy stops evolving, which means an optimum has been found (not necessarily the optimum because the "performance surface" could have multiple peaks and an evolutionary algorithm will climb only the nearest peak from where the strategy starts. Like I said, I've always been interested in these but I haven't really done them but smart engineers are using these to design all sorts of cool toys.

Still with me? Here is where any of this has to do with solitaire. When I first got my smart phone last year, I started playing (for the first time in my life on a computer) klondike solitaire (three cards dealt and three rounds through the deck) and noticed that my winning percentage increased. That is, I was getting better or more skillful. Prior to this I had only played solitaire with a brick and morter deck of cards and I would have argued that there is no strategy, a win is all in the luck of the shuffle. Anyway, I developed a serious addiction and took the game off my smart phone.

Then I got my ipad, which I had for about a month before I downloaded a klondike solitaire game. I'm absolutely fascinated with the strategy. Enough that I thought, I could spend a day programming a solitaire solver and then explore a strategy space and try to determine the optimal strategy. And then I thought, I could learn something about evolutionary algorithms by implementing one. I did a little google and google scholar search and found that a few mathematicians have addressed solitaire but not many. Some of these address a very basic question, how many shuffles are winnable? This problem is way too hard for an analytical solution (first it is dependent on a specific strategy but its too hard even given that).  That's an interesting question but I'm more interested in strategies. For example, if I just dealt a 4 clubs and I have a six of spades as the top card in my building stacks and a five of hearts up top in my suit stacks, do I move the five of hearts down to the build stacks so I can play the 4 of clubs? I have one card less in my suit stack (so I'm further away from winning) but I have one more card in my build stack (so I'm closer to winning) but certainly there is more of a cost to pulling a card from a suit stack than gaining a card in the build stack so...what's a computational biologist to do?

Write some code. I don't mean writing code for ME to play solitaire I mean write code for the COMPUTER to play solitaire. Sort of like Deep Blue. What I thought would take a day has taken about a week and lots of intense hours. I'll say this, even the simplest "strategy" requires a lot of decisions that we don't even think of as decisions. But you are forced to recognize them when you're coding the game. My initial strategy is pretty dumb as it cannot see ahead more than 1 step and evaluate the consequences (so if I see an ace as card 2 in the three cards that I've just dealt it may be worth moving a card down from the suit stack to the build stack to be able to play the top card - and therefore the ace):

definitions
1.The build stacks are the 7 columns of face-up cards that you build in descending order with alternating color
2. The suit stacks are the 4 columns of single suit cards that are built in ascending order (if completed the game is one)
3. The talon is the single pile of face up cards that can be played to the build or to the suits
4. The pile the the single pile of face down cards that are turned over, three at a time, and added to the talon.
5. The down stacks are the face down cards beneath the build stacks

The strategy, in order of priority:
1. play the build cards to the suit stack
2. play the talon to the suit stack
3. play build kings to empty build columns with priority (the first king moved) given to the king on the build stack on top of the shortest down stack
4. play talon kings to empty build columns
5. play one build column to another with priority (the one being moved) given to the build stack on top of the shortest down stack
6. play the talon to the build stack

So there is 1) no moving parts of a build stack to another build stack (to free up a card that can move to the suit stack, say) and 2) no moving suit stack cards back to the build and 3) no choosing not to do one of the above (such as not playing a talon card). I would consider these three more advanced strategies but each has lots of flavors. At this point I may be satisfied with simply having coded the computer to win a game because implementing more advanced strategies would be even more of a time waster.

Which raises the question, can I make money out of this? Probably not. My dumb computer has a winning percentage of about 1%, which seems awefully low, even for this simple algorithm. By comparison, I've won 17% of the 1100 games that I've played on my ipad. Maybe I'll try to create an evolutionary algorithm and let it evolve a more optimal strategy.

postscript. At Twin Brook tonight Ian said he got through most of this post before he realized not only was I taking my time relating this to running but I probably wasn't going to ever get there. So here is the connection: This is the sort of crap I think about when I run solo!

Here is my computer's first win! (what is shown is the top card of the build stacks from start to finish)


  playmap(htops[, 1])  X1  X2  X3  X4  X5  X6  X7
1                start  H3 D11 C13  C7 C10  C2  D2
2       build to build  H3 C10 C13  C7  D6  C2  D2
3       build to build  H3 C10 C13  D6 H13  C2  D2
4       build to build  C2 C10 C13  D6 H13  S5  D2
5       build to build  C2 C10 C13  S5 H13  S2  D2
6       talon to build  C2 C10 H12  S5 H13  S2  D2
7        talon to suit  C2 C10 H12  S5 H13  S2  D2
8        build to suit  H3 C10 H12  S5 H13  S2  D2
9       build to build  S2 C10 H12  S5 H13 H10  D2
10      talon to build  S2 C10 H12  S5 C12 H10  D2
11      build to build  S2  S3 H12  S5 C10 H10  D2
12      build to build  S2  D2 H12  S5 C10 H10  C6
13       talon to suit  S2  D2 H12  S5 C10 H10  C6
14      talon to build  S2  D2 H12  H4 C10 H10  C6
15      build to build  S2   . H12  D2 C10 H10  C6
16           play king  S2 H12  D1  D2 C10 H10  C6
17       build to suit  S2 H12  D3  D2 C10 H10  C6
18       build to suit  S2 H12  D3  S3 C10 H10  C6
19       build to suit  S2 H12   .  S3 C10 H10  C6
20           play king  S2 H12 C10  S3  H6 H10  C6
21      talon to build  S2 H12 C10  S3  H6  S9  C6
22       talon to suit  S2 H12 C10  S3  H6  S9  C6
23       build to suit  H3 H12 C10  S3  H6  S9  C6
24       build to suit  H3 H12 C10  H4  H6  S9  C6
25      talon to build  H3 H12 C10  H4  H6  H8  C6
26      build to build  H3 H12 C10  S8  H6  H4  C6
27      talon to build  H3 H12  H9  S8  H6  H4  C6
28       talon to suit  H3 H12  H9  S8  H6  H4  C6
29       build to suit   . H12  H9  S8  H6  H4  C6
30       build to suit   . H12  H9  S8  H6  S5  C6
31      build to build   . H12  S8 C11  H6  S5  C6
32      build to build   . C11  S8  D5  H6  S5  C6
33      build to build   . C11  S8   .  H6  S5  D5
34      build to build   .  S5  S8   .  H6 D13  D5
35           play king D13  S5  S8   .  H6  C9  D5
36      talon to build D13  S5  D7   .  H6  C9  D5
37      build to build D13  S5  D5   .  H6  C9 S12
38      build to build S12  S5  D5   .  H6  C9  S4
39       build to suit S12  S5  D5   .  H6  C9  D9
40       build to suit S12  D6  D5   .  H6  C9  D9
41      talon to build S12  D6  C4   .  H6  C9  D9
42       talon to suit S12  D6  C4   .  H6  C9  D9
43       talon to suit S12  D6  C4   .  H6  C9  D9
44      talon to build S12  C5  C4   .  H6  C9  D9
45      talon to build H11  C5  C4   .  H6  C9  D9
46       talon to suit H11  C5  C4   .  H6  C9  D9
47       build to suit H11  C5  D5   .  H6  C9  D9
48       build to suit H11  D6  D5   .  H6  C9  D9
49      talon to build H11  D6  D5   .  H6  C9  C8
50      talon to build S10  D6  D5   .  H6  C9  C8
51       talon to suit S10  D6  D5   .  H6  C9  C8
52       build to suit S10  D6  C6   .  H6  C9  C8
53       build to suit S10  C7  C6   .  H6  C9  C8
54       build to suit S10  C7  D7   .  H6  C9  C8
55       build to suit S10  H8  D7   .  H6  C9  C8
56       build to suit S10  H8  S8   .  H6  C9  C8
57       build to suit S10  H8  H9   .  H6  C9  C8
58       build to suit S10  H8  H9   .  H6  C9  D9
59       build to suit S10  H8  H9   .  H6   .  D9
60      build to build  D9  H8  H9   .  H6   .  H5
61       build to suit  D9  H8  H9   .  H6   . S13
62       build to suit  D9  H8  H9   .  D8   . S13
63       build to suit  D9  H8  H9   .   .   . S13
64       build to suit S10  H8  H9   .   .   . S13
65       talon to suit S10  H8  H9   .   .   . S13
66      talon to build S10  H8  H9   .   .   . D12
67       talon to suit S10  H8  H9   .   .   . D12
68       build to suit S10  S9  H9   .   .   . D12
69       build to suit S10 H10  H9   .   .   . D12
70       build to suit H11 H10  H9   .   .   . D12
71       build to suit H11 H10 C10   .   .   . D12
72       build to suit H11 C11 C10   .   .   . D12
73       build to suit S12 C11 C10   .   .   . D12
74       build to suit S12 C11 D11   .   .   . D12
75       build to suit S12 H12 D11   .   .   . D12
76       build to suit S12 C13 D11   .   .   . D12
77       build to suit S12 C13 C12   .   .   . D12
78       build to suit S12 C13 H13   .   .   . D12
79       build to suit S12   . H13   .   .   . D12
80       build to suit S12   .   .   .   .   . D12
81       build to suit S12   .   .   .   .   . S13
82       talon to suit S12   .   .   .   .   . S13
83       build to suit D13   .   .   .   .   . S13
84       build to suit   .   .   .   .   .   . S13
85       build to suit   .   .   .   .   .   .   .

managing calf pain

The evidence for what works in managing sports injuries is one of the more frustrating areas of health-related research that I've come across. During my MP run 16 days ago, I got a sudden calf pain that felt something like a cramp. At the time I didn't think it was a cramp because my gastrocnemius muscle (at least) wasn't obviously balled up. But maybe it was the deeper soleus. I assumed it was some sort of muscle strain (tearing). My management included no stretching, no strength training, no massaging, no nsaids, no icing, and no heating but only initial rest then running with short walk recoveries (note on my pain scale: 3 is noticeably sore, 5 is painful to run, and 7 is painful enough to not run, and 9 is painful enough to want to amputate). The initial pain was a 7.
S - off, sore
M - off, sore
T - 2.2 miles alternating walk/jog every 1/3 to 1/2 mile, pain = 2-3
W - attempted to run back cove 5k at 8 min/mi but at mile 1.1 pain went from 2-3 to 4-5. Continued walking/jogging rest of 5K with pain at 4, no soreness in evening
Th - 3.7 miles at back cove. Ran (7:35-8 m/m) 3.1 miles at pain=1-2 then sudden jump to 4-5. Walked remaining 1/2 mile, no soreness in evening
F - 4.8 miles on Brook rd (mostly flat). Ran (8 m/m) 3 miles at pain = 1-2 then sudden jump to 4. Walked most of rest with some light jogging. Sore (pain=1) that evening.
S - 4.8 on Brook Rd. 4 x 1 mile with 1/4 mile walk recoveries. Pain = 2. worked well.
S - off
M - 3 x 2 miles (7:12-7:59 m/m) @ back cove with 1/4 mile walk recoveries. Pain = 1. noticed pain on stairs before though (much more than running). Speed didn't seem to aggravate soreness.
T - off
W - 7.7 at RIT perimeter rd. 3 x 2.5 miles with 1/8 mile walk recoveries. Progression: 7:40 7:13 7:10 6:42 6:32 6:21. Last 1/3 at 6:08. Pain = 0.
Th - 4 + 2.5 + 1.5 mile with 1/8 mile walk recoveries. Brook Rd. Pain=0 first 6 mi then =1 last two.
F - 3 x 2 miles with 1/8 mile walk recoveries. 1st 3 miles community park trail last 3 on road. Progression: 6:42 6:48 (long hill) 6:22. Pain = 0
S - 10.5 very easy miles at Bradbury with several very short walk breaks. Pain = 0
S - 13.1 road (Woodville/Woods/Winn) at 7:30 min/mi with 4 1/8 walk recoveries every 3 miles. Pain = 0


So while I cannot say that the run-walk strategy was necessary for effective management (since I didn't try continuous running, at least after day 4), the run-walk strategy at least allowed me to run decent mileage and even some fast miles. To be continued...

pop

Pop is not a good word for a runner. I have heard many people describe various achilles/calf injuries as occurring with a sudden "pop" and I never could understand that until now. No my achilles didn't rupture but while running up a climb on my MP run this morning my calf went pop and I suddenly was barely walking. I flagged a car and borrowed a cell phone to have Cacky pick me up. No injury has ever stopped me from completing a run, not even my metatarsal stress fracture. The feeling and suddenness was like a charley horse but it wan't from muscle cramping.

The choice to run MP, especially on the Woodville loop, was probably unwise. Inspired by Brad Hudson, I did my first 8s hill sprint wednesday. He recommended starting with one but I of course started with 3 (its only 8s!). My legs were surprisingly sore Thursday. But, not heeding this warning, I did a 2 x 10 min tempo interval at Twin Brook thursday afternoon. It was not my best effort. Then yesterday I did what was supposed to be an 8-10 mile easy run but decided to check out all the new single track at Blackstrap "community forest". I did exactly 9 miles at 10:45 pace and I was more tired than running the Bradbury Breaker. The hills are very steep and, like all Escher designed trails, there is more climb than descent.

Then I followed up this "easy" run with the MP run today. I was planning on doing this on Rt. 88 (Maine marathon course) since it is flattish and I can assess the my pace with how I'm feeling but I was too impatient to drive and just did the Woodville loop from my home (which is much hillier). Not surprisingly running at MP pace after a not terribly good workout thursday and my not-easy day yesterday was a mistake. I was miserable by mile 2 at MP. Luckily, my popped achilles ended the misery.

Just run, baby

Ever since my first Mt. Washington, I've been intrigued by the performance differences between running and walking steep climbs. Without diving into the research, I did my own experiment (non-randomized, two replicates that are confounded with year) using the summit trail of the Bradbury Mt. Breaker. First, here are my splits from 2010 and 2011. The 2010 splits come with an asterisk as I went off-course for 2:41 but I've removed that from all the data below (I'm still trying to hack into cool running so I can remove it from the results as well).

The first two miles were respectably faster this year than last year (a goal). During the first mile I felt like I was going the correct pace but I was questioning this because a group that I knew I'd be passing started even faster than I. By 3 miles (1/2 mile over the top of the summit) I had lost the time gain and was dead-even with the previous year and basically maintained this through the first 5.25 miles. The next three miles, and especially the 2nd climb up the summit trail were painfully slow compared to last year. The only bright spot over the last 3.5 miles was the last 1/2 mile which I first was pushed by and then pulled by Jeremy, who I was glad to have along for the ride to the finish.

The major difference between years seems to be the summit trail. Last year I ran almost all of the summit trail on lap one and most on lap two. This year I had decided to walk most of the summit trail and save my energy for the descent. Part of my reasoning came from talking to others and part came from a paper that I had read that used O2 consumption data to argue that runners climb too quickly and descend too slowly (of course these were on grades of only a few % - not 25-40% like the summit trail).

What was interesting, and I noticed during the race and commented on to several people afterwards is that I didn't feel any fresher after having walked the summit trail than after running it last year (at least as far as I can remember last year). Running it slowly or walking it quickly doesn't matter; the summit trail is a lung buster.

So I looked at my splits climbing the summit trail (starting a wee past the aid station) and the 3/4 mile descent down the other side to see if walking the summit trail allowed me to descend faster (unlike the switchback or S. Ridge trail, the Tote Rd? descent from the summit can be as fast as you want it to be). Here are the data:

On the first ascent, in which I ran the flatter sections and made the effort to walk the rest, I lost 8s to 2010. But then I lost 16 seconds on the descent! The second time around, in which I walked all of the summit trail, I lost a whopping 17 seconds on the climb and still lost 6 seconds on the descent. So these data suggest that no, walking not only slowed me down going up but slowed me down further going back down!

I talked to Judson Cake after the race and asked if he walked any of the summit trail and he said no, only because he finds it hard to transition back into running. The 2 sec that I walked at Mt. Washington in 2009 I had the same feeling, and decided I'd be faster running the whole thing. Is there something physiological to this or is it only mental (yes I recognize that mental is physiological but I know what I mean). One caveat to these results is that I never walk in races because I don't really do any races that this is necessary. So I never practice fast hiking and in fact Jamie, and Ian, and Stephen, and probably everyone else are much faster hikers than I. So maybe an experienced fast hiker would have different results but I'm not practicing fast hikes for 5 minutes of one race. I'd rather just run, baby.

1/2 full or 1/2 empty?

B2B 2010: 37:24
B2B 2011: 38:00

1/2 Empty: 1 minute short of my goal time at B2B based on MD5K
1/2 Full: Placed 180th (27th master) v. 193 (31st master) in 2010
1/2 Empty: Felt like crap by mile 3.5
1/2 Full: Finished race
1/2 Empty: Based on WAVA, should have been only 17s slower than 2010 because of age increase
1/2 Full: male runners over 35 y.o. and in top 400 who competed in 2010 and 2011 were, on average, exactly 1.0 minute slower in 2011 than 2010 (N=61) (mostly due to humidity and sun)
1/2 Full: Taking into account age and conditions, I was 24 s faster this year!
1/2 Empty: I don't accept aging so removing that, I was only 7s faster than 2010 taking into account only the conditions
1/2 Full: I was 7s faster than last year!


File under: How to Lie with Statistics

Training week 6/19 - 6/26

M 5.1 mi failed tempo on beach - 2 x 1 mile at 6:50/mi, St. Augustine beach

T 7.1 mi road easy, St. Augustine beach (7:32/mi)

W AM 5.3 mi failed road interval 4 X 800 (2:54 2:54 2:54 2:56) + 2 x 400 (1:29 1:30)

     PM 4.8 mi road easy (7:21/mi) St. Augustine beach

T 4.5 mi easy St. Augustine beach (7:26/mi)

F AM 5.4 mi easy @ Back Cove (7:21/mi)

    PM 6.2 mi, incl. 4 mi tempo (6:54/mi) @ Twin Brook

S 10 mi easy @ Bradbury (9:47/mi)

S 15.3 mi road easy (7:38/mi)

Total distance - 63.6 mi

injury report: stepped on a rock during a short road last Friday (9 days ago) and bruised my right forefoot (I was running in the Asics Pirahnas which have thin foam soles). This didn't bother me on the roads in Florida but the gravel at back cove and the roots at Bradbury absolutely killed me.

Once a runner sequel

Short sequel to "once a runner":

Chapter 1. Too hot to run

Chapter 2. Too hot to run

Chapter 3. Too hot to run

Chapter 4. Too hot to run

Chapter 5. Running in Florida sux. I'm retirin' from milin'

Life has brought us to Florida this week and the family is staying at my parent's house in St. Augustine Beach. I ran 8 1/4 miles last night along A1A starting a little after 9PM and it was still 88-90F! But that was pure pleasure compared to my 5 mile beach run this morning at 8:30AM. It's just too hot to run on the beach and the sun is too strong.

Here are the numbers for last week

M rest day

T PM1: Back Cove easy (7:27/mi); PM2 TMR TNR easy + 2.5 at MP

W 9x300 @ 2-3K pace @ Back Cove, 7.1 total

T 8.5 easy on Piscataqua Trail (8:46/mi)

F 8 at Twin Brook incl. 3 at 1/2MP

S AM: 11.1 easy at Bradbury; PM: 4.8 east on Brook Rd (7:51/mi)

S PM: 8.3 easy (7:48/mi)

Total distance: 60.5 (that's good for me given 1 rest day and no run longer than 11)

Total time: 8:47

road kill

Poor time-management skills on my part in combination with Cacky's birthday, my parents visit, and three functions related to Sam's HS graduation conspired to keep my away from the trails this week. The only upside is the Woodville/Field rd. loop is mostly dirt shoulder and cars are rare. Monday was a planned rest day. Wednesday was not. I almost missed thursday too but snuck out for a late night interval workout while running home from FHS awards night.

M rest

T PM1 - 4.7 easy@back cove; PM2 - 8.1 @ TMR TNR incl. 2.5 miles at tempo

W rest

T 7.6 interval (4 x 1200 @ 5K), woodville rd.

F 8 easy incl 8 strides, woodville, 

S AM 1.5 w/u + 5 mile race (30:11); PM 4.1 recovery, Brook rd.

S 11.1 easy, Woodville rd.

Distance: 50.2, including 3 workouts. Not a great week mileage-wise but given the 2 rest days and all the competing activities I'll take it.

Run for Honduras 5 mile road race

I've been busy with my research and Cacky's birthday (she just turned 29!), Sam's graduation and have not had much patience for taking the time to trail run so I've resorted to three road runs over the past 6 days, which is more road running than I've done all spring. My goto road run includes the Woodville-Field Rd. loop, which has few cars, a beautiful dirt shoulder, magnificent farmland scenery, and sweet rolling hills (it drops and climbs, drops and climbs from the East branch of the Piscataqua River). Thursday night, I still hadn't run and had little time left, so I banged out a 7.5 miler on this loop that included a 4X1200 at 5K pace. And yesterday afternoon, similarly pressed for time, I did an easy 8 mile run using the loop. But after this run, I decided that I needed to take the time to return to the trails.

Cue forward a few hours and I decided to race the Run for Honduras 5 mile road race which uses the same Woodville loop. This decision was made after I was reminded that my son Tom was running it and he pre-registered a few weeks ago. Son Will also decided to run it. McMillan has my 5 mile time at 29:33 but I was not gunning for this time given the course and my workout only 36 hours earlier. I figured 6 min/mi and 30:00 would be a good run.

The race is organized by the Foreside Community Church and the Falmouth Congo Church and raises money to provide basic health care for rural hondurans. The FHS track coach legends Danny Paul and Jorma Kurry encouraged the track kids to race this since a FHS track alum had something to do with organizing it so I figured there'd be lots of FHS runners and alum but it was mostly members of the churches I think.

After an easy 1.5 mile warmup and change into my race shoes I arrived at the start line and didn't really have to push my way to the front because the front consisted of two boys that were maybe 10-11 and a skinny post-collegiate-runner-looking guy who turned out to be Nathan Huppe from NH (not sure what about this race attracted him!). The gun went off and the two kids and Huppe went out fast. Not wanting to be seen running behind two middle schoolers, I went out fast too and was on about 5:35 pace after a quarter mile and was in control of 2nd place. I decided to slow it down a little and hit mile one in 5:59. That was a little too slow because mile one drops about 80 feet to the Piscataqua River. I could hear footsteps behind me for only the first half of the first mile and was maybe 150 m behind Huppe so from here on out I'd be running alone. The course went around the Woodville/Field Rd loops clockwise so mile two was a climb of about 100 feet (total climb of around 130') and I went through that mile in 6:19. Mile 3 drops sharply down to the river and climbs a bit (5:57). At this point I was feeling the toll of the hills (or my workout) and still had a long climb and I was alone in 2nd place with 1st place 400 m ahead and 3rd place was out-of-sight behind me. That is, I had little motivation to push it to the limit. But I continued the race and hit mile 4 in 6:12, which isn't bad considering it was all climb up from the river. The last mile is pretty typical road race flat; my split was 5:45 for a 30:11 2nd place finish. Will had a good race (35:11) but Tom seems to have inherited my susceptibility to sidestitches and got one by mile 2 so jogged in in 39:59).

Results are now up

The organizers served up a yummy Honduran breakfast burrito filled with egg, cheese, refried beans, and fried plantain with cantaloupe on the side.

Weekly training 5/30 - 6/5 2011

Moved from Pineland phase (Daniel's tempo + hills + long run) to summer-of-malmo phase

M 5.2 easy @ Pineland
T AM 4.2 easy @ Back Cove w/ 10 strides; PM 7.7 easy @ TMR TNR
W 7.9 @ Back Cove  w/ 4 X 800 @5K (2:50, 2:52, 2:52, 2:54)
T 5.1 progression @ Back Cove
F 9.4 easy @ Back Cove and East End hills
S 6.1 easy @ Bond Brook (hilly!)
S 11 w/ 4.5 mile tempo @ 30K pace

Total mileage 56.5
May mileage 205.8
Year mileage 622

Is that a snake in your pocket or are you just happy to see me?

I missed the Pineland run this morning because I wanted to be sure Son #1 had everything he needed today for his double header: 1) State Outdoor T&F meet in Augusta (he ran 4X8 and 800) and 2) Camden-Rockport HS prom. Cacky and I watched the FHS 4X8 team sail to second place with a really great run and we had about 4 hours until the solo 8 so we headed out to Bond Brook Recreation Area, which I had heard alot about because they hired John Morton to design a Morton Trail for xc ski racing (Pineland, Libby Hill, and Twin Brook are also John Morton Trails).

The parking area is in the back of a cemetary next to the airport. Good luck finding it. The entrance trail drops about 100 feet in a very short distance and would be wicked fun in skis or snowboard or cafeteria tray. I started on the blue loop which was typical pineland then cut over to a red loop, which was cut but not cleared. The slash was difficult to run on and the trail went dead straight down what I'm guessing was a 30% grade. If this becomes a ski trail I cannot imagine going either up or down it. The cut of course dead ended at the bottom of the hill so I turned around to run (mostly walk) back up the slash and return to the blue trail. I then took another detour off the blue trail which was a very grown over road with a big washout much of the way down. The road just dropped straight down to Bond Brook. Near the bottom was the red marked trail and looking at the map I was not far from where I'd just been but it wasn't cut yet. Bond Brook is a beautiful, large creek but really none of the ski trail follows it so I turned around to again climb what I had just descended and returned to the blue trail. The blue trail continued to climb until I noticed I was on the other side of the water towers by the parking area, which was the high point in the system.

From the high point, the trail dropped through the "halfpipe" which I'd heard alot about because some college racers had some trouble with it this winter. No duhhh! The half pipe was indeed a natural ravine and the trail snaked its way up one wall and then the other and then back as it descended down. I have to give the Augusta Trails group some credit for having the balls to put this into their trail system. Anyway, because it was a little too much, they are spending some time this summer taming it, which is a little too bad because I know a dozen FHS skiers who would love to ski it as is.

In all, I got a 6 mile run in with 1150' total climb. Ian said there is a race here later in the summer. I predict some carnage on this course.

Cacky and I walked around a bit to enjoy the weather and a beautiful Eastern milk snake was sunning itself on the trail and quickly slithered into the grass cover. He was easy to catch but was a little feisty and snapped at the air for a minute. Milk snakes and rat/corn snakes are usually quite mild and gladly curl up around your arm but even after he stopped snapping he never really calmed down. Maybe it was my sweaty arm? Cacky got my phone and took a few photos.

We worked in the car for a while at Bond Brook (ok some of us surfed the web and fb on our phone) and then returned to the track meet to watch Sam in the solo 8 and then see him on his way to Camden. With more days like these, I'll stop looking for summer camps in New Foundland.

2011 Pineland Farms 25K race report

1st 5K: Fast
The first 5K was rocket fast. Actually I thought the leaders went out quite conservatively. It was the chase pack of about 6 (what do you call the 2nd pack that has no chance of catching the lead pack?) that went out a little fast. My goal was 10s/mile faster than last years pace. Instead I was 15s/mile faster. I was in 10th or 11th place at the 5K marker. The only one in the pack that I recognized was Nathan Alsobrook, who I couldn't keep up with over the O trail at the Bruiser last summer.

2nd 5K: Where'd everyone go?

On the climb to the yurt, I kept pace but the pack slowed. By the time I left the (super awesome) yurt aid station, I was alone in 6th place with Peter Sedgwick about 10-15s on me. At some point in the farm field behind the yurt, Ben Schaeffer (age 18) caught me and we ran together for a few miles. Apologies to Ben for not being more talkative but I really wanted to avoid getting a sidestitch! By the time we were 1/2 way around the farm field we had put quite a lead on the pack that we had just been in. Where'd they go? We passed Peter on the first hill into the Valley Farm loop. For this split, I averaged 8s/mile faster than 2010 but this included a really slow mile 5

3rd 5K: Running alone
Ben stayed with me until the last pass through the yurt (totally awesome) aid station but fell back at the yurt. After this, I was in 5th place, running alone and with no visible runner in front or behind me. Feeling good but I was clearly dropping down to my 2010 pace.

4th 5K: Wheels come off
I made it to the Grove with a sub 1:50 pace, which was my goal but the cloverleaf part of the Campus loop did it's damage - I was balancing on the knife edge of a side-stitch. I focused on breathing and made it to Oak Hill in good shape. Soon after the little field section in Oak Hill, the stitch escalated enough that I was worried. I was in 5th place and didn't want the stitch to escalate into the debacle from 2009 so I fully stopped and did about 40s of deep breathing bending over and stretching, then got on my way and feeling quite good. And I was still running alone with no visible runners behind me.

5th 5K: And the axles too
On the gradual climb in the Gloucester Hill loop the stitch was knocking on the door again. I stopped again and repeated my bending over and stretches - again 35-40s. Just as I was ready to run again, Denis Tranchmontagne caught me. I started running again and re-passed him. Very soon after passing him the stitch knocked again and I stopped again. Another 35-40s of stretching and breathing and Stephen Wagner passed me. He was looking pretty strong too. I took off and hung with him and we caught Tranchmontagne. I stopped at the Oak Hill aid station for water (I didn't want to drink the water while running because this screws with my breathing and that would induce the stitch). By the time we ran out of Oak Hill onto the final field I was maybe 20s behind Tranchmontagne and 40s behind Wagner. I picked up the pace some but didn't really begin to press until the turn at the bottom of the field. By the top of the field I caugh Tranchmontagne but couldn't catch Wagner.

Results
3rd year racing this and I've yet had what I think is a really good race. I got a 1 minute PR but failed to go sub 1:50, which is disappointing. I never let my stitch escalate into unrunnable pain but stopped to let it subside. I had about 2 minutes of stoppage so this cost me my sub 1:50. Or maybe it saved the race because I was 6th overall, which is a bit surprising, especially given the depth of the field last year. Unfortunately I was 5th in my age group (WTF?), so didn't take home any hardware. BUT we did take home the 25K team award and Acidotic Racing graciously rewarded us with a case of Red Hook ESB. Thanks guys!

Conditions
Brutally humid. 'nuff said.

Achilles rapture

I've solved the mystery of my achilles pain last Friday. It raptured. No, not the whole tendon! Just it's soul. Clearly, the wonkiness that I felt Wednesday was my achilles' soul preparing to rapture its bonds from its corporeal host. The slight soreness on Thursday was the beginning of the rapture. And the pain during and after the run Friday late into the evening was the climax resulting in complete freedom and presumably its ascension into outer space on Saturday May 21. I say, good riddance, cuz now I'm running pain free and have been all week.

Some other bodies raptured too.

Haze in the barn

Well it doesn't look good for Sunday's epic 25K battle amongst the cattle. I've managed to get achilles tendinosis and the progression has been rapid: wonky on wednesday, sore thursday, and painful friday. I will start x-training Monday, including pool runs, rowing, and roller skiing. I will probably try to do a little run late in the week for a last-minute test but I'll likely be conservative regardless and not race.

M Rest
T tempo @ Twin Brook (6:49 6:46 6:36), 9 mi total
W 8.3 ez @ Back Cove
T 8XSkillins hell repeats, w/ mountain goat Jeremy. 8.2 mi total
F 6.1 ez @ Yarmouth roads

Total distance: 31.6 miles

Long and Hard

This will be my peak week prior to Pineland. 61 miles and 3 workouts. All following the 5K on Sunday. Legs were tired through thursday but the recovery run on Friday did it's job. I realized that I don't put in enough race pace training runs before Pineland each spring and its kinda late now but I got one in today.
M 6.4 easy @ twin brook (7:55/mi)
T 8.7 tempo @ twin brook (6:38 6:40 6:30) - tempo felt tough
W 6.2 wu + 3.1 junk pace + 0.3 cd @ back cove 5K. junk pace was too fast (7:02/mi) given sunday's race and tuesdays workout
T 6.8 skillinz hell repeats (2:54 2:53 2:54 2:56 2:54 2:51) lungs good, legs sore about 2/3 up each climb.
F 6.6 recovery @ back cove (7:51) including some kick-butt & high knee drills
S 9.2 ez @ pineland (8:40/mi) including 8 strides
S 14.2 @ pineland - 9 ez (8:13/mi) + 5 @ RP (7:03/mi)

Distance: 61.5 mi
Time: 8:11:25

Mother's Day

Ran MD5K this morning and pulled off a PR by 8s (17:50). My last road 5K was the same race last year (17:58). I think I ran the race a little smarter than last year, which may account for the 8 extra seconds, but I'm hoping that it's actually better fitness. I guess time will tell. Most of the Dirigo guys were out for a training run and spectating and/or aged-up to M50-54 so I had what I think is my first ever age-group win in a road race. The first mile, which has a long downhill from the start, was right on target (5:45) but required a little squeezing through groups of young kids that went out too fast. Scott Hornney and I traded pulling on mile two (5:51), which was mostly a gradual climb and I guess about on target. Around Mile 2 I pulled a little ahead of Scott and Lonnie Renny pulled ahead of me. Mile 3 (5:42) is mostly gradual descent and I thought I could do this about 5-6s faster but I did manage to hang on to Lonnie pretty well. Sadly, I think the 5K is my best distance and I might actually race a couple more of these this season. I might even train for it by throwing in some faster speedwork. My groin hurts just writing that.

Time 17:50

Overall: 19/2459

Division: 1/76

But the really big news is...I did my first ever training run on a track this wednesday. I geared up to go to Back Cove for a cut-down but it was raining and I didn't feel like driving there so I went to the Falmouth Track instead! I don't think I'll make a habit of it. The Lacrosse team was practicing during my workout and I had lots of balls whizz past me everytime I ran one end of the track. I felt like I was in an arcade game.

Training week:

M Rest

T TMR TNR @TB 8.8 mi easy + 2X1/3 mi "sprints" (7:51)

W cut-down 3K + 1.5K + .75K + 0.375K @ 6:10 5:57 5:43 5:11, total 6.1 mi

T 8.1 mi road easy (@7:27)

F Rest

S 8.3 mi very easy Pineland (@8:51)

S AM: MD5K (17:50 5:45+5:51+5:42) + 1.7 mi wu

    PM: 8 mi road recovery (@7:50)

Total Distance: 44.2 mi

Total Time: 5:39:53

Training Week 4/25/11 - 5/1/11

M Rest
T 8.8 m tempo intervals @ TMR TNR, 2 x 2mi 7:24 6:53 6:29 6:53
W 8.6 m easy (7:32/m) @ Back Cove with 8x strides
T 8.0 m hell repeats 3 x bitch (2:31 2:30 2:3x) + 5 x Skillins (2:59, 2:59, 3:00, 2:58, 2:55)
F 6.3 m easy (7:22/m) @ Brook Rd.
S 14 m easy long (8:24/m) @ Pineland (w/ 6 barefoot strides)
S 8.6 easy (7:55/m) @ Pineland (2 x Oak Hill)

Total Time: 7:18:26
Total Dist: 54.3 m

No aches. No pains.

start of "Weekly Training" posts

I've decided to post my weekly training summary in compact format. Its largely for my use but will also be open for anyone else to check out. I enjoy the occasional scan of other runners weekly training summaries to see how they are training. And its a lot easier to get a quick review than going through daily reports. LRC has a nice marathon training thread that is full of these with discussion, which I've found useful.

M Boston Marathon - logged as long run, fast-easy pace  3:16:19  26.42 mi
T planned rest
W unplanned rest (it was cold and rainy and I was lazy)
T Back Cove easy 55:13 7.2 mi flat
F Jungle Run easy 1:18:38 8.6 mi hilly
S Pineland easy 1:22:12 9.4 mi mod hilly
S Back Cove/E Prom easy 54:09 7.2 mi few short, steep hills


Totals
Time 7:46:24
Distance 58.8 mi


My goal for Boston was to not let it interfere with my training and all data to date point to "Mission Accomplished". Legs were fresh for all four post-marathon runs. Today (post run) is the first day that they feel tired, but its been 7 months since I've run more than 50 miles in a week.


A little picture of the new trails at the east end, portland

Cheers

Photo courtesy of Steve Wolfe

Notes: My goal going in was to run even 7:50s with an occasional faster mile just to add some fun.

Distance Cumlative Split
5k 0:22:56 0:22:56
10k 0:46:54 0:23:58
15k 1:10:28 0:23:34
20k 1:33:51 0:23:23
25k 1:57:07 0:23:16
30k 2:20:49 0:23:42
35k 2:44:01 0:23:12
40k 3:06:38 0:22:37
Half 1:38:48 1:38:48
Finish 3:16:16 1:37:28

5K - Everyone is flying by me as I'm trying to apply the brakes. I'm hitting 7:20s with the brakes to the floor.
10K - Everyone continues to pass me. Mile 5 was 7:52 but I averaged about 7:40 over this split. By the end of this split, I decide that 7:30s is a pretty easy pace.
15K - Still being passed by most everyone. Jamie caught me just shy of mile 8 and I ran about 1K with him at 7:08ish pace. He looked awesome and continued on while I returned to my 7:30s.
20K - I'm finally not being passed. The Wellesley rush pushed me to around 7:20 for 2 miles.
25K - meh. My feet are sorish but I'm not at all tired. A little bored.
30K - Newton hills - Now I'm passing lots of people. The hills give me some energy.
35K - With about 12K to go I entered the zone. 7:20s are feeling good and I'm passing even more people. The heartbreaks are everywhere. From Boston College in is an absolute rush - the crowd just slings you along.
40K - With 5K to go I thought I might put the hammer down and go for 3:15. Mile 23 was 6:59. Yeh, I don't need that. Slow back down to 7:20s. Still passing lots of people.

Felt very easy until my tempo mile at 23. Left foot had about five very short bouts of cramping over last 4 miles that I thought was going to end my race but these never fully blossomed. The first 15 minutes after the finish absolutely sucked. My legs were thrashed. I wanted one of those wheel chairs. Surprisingly my quads were not sore, in fact my quads were never really sore during or after. But my legs slowly recovered and then it was mostly my feet for about an hour. But these recovered too and I now feel pretty good. I'm pretty sure I'm retired from marathoning for a while.

It was great to see Jamie before and after and missed him at our celebratory pizza and brew at Picco with Cacky and Joe. Jamie had a great PR. Chuck and Katie both had awesome runs. And Joe's triumph was simply running after bad achilles tendonopathy only 3 weeks ago.

Morning Report update - absolutely no soreness. Not getting out of bed, not when pushing a finger into my muscles. This is stunning considering that I could barely walk for about 15-20 minutes post finish.

Reverse Taper

You won't find this in a marathon training schedule:

My ramp-up for Pineland training has transmogrified into a reverse taper for Boston. After today I've now got long runs of 16, 11, and 10 miles since October 1st! While everyone else is tapering, I'm just trying to get back into some kind of running fitness (which seems to be working well enough). My focus has been on hills including a short, fast hill climb up Hatchet Mountain in Hope ME:

10 hill repeats up the Skillins Tree Farm off Blackstrap Rd:

And 8 hill repeats up the first bitch (same ridge as above but about 1/2 mile south of Skillins):

Now I'm ready to just cruise this week with about 35-40 miles of easy runs. I don't know my Boston Strategy other than not race it. My original plan was to run it in 3:30 but since the M45-49 qualifying time is now 3:25 I think that will be my goal. Probably run every 5th mile (starting with the first) in 7:30 and everything else around 8 min/mile. But talk is cheap...even for a training run.

Merrimack River 10 mile trail race 2011 report

Absolutely. Perfect. Weather.

Trail Monsters Four, Andy, Ian, Emma, Chuck, Don, and I crossed state lines for the season opening Merrimack River 10 mile trail race. This race really is a must do every year because the field is top notch and the race is old school cool. Don and I did a 2 -2.5 mile warm up and I noticed several overgrown sections of the trail with skin-piercing brush. I stopped to break the eye-gouging branches (to those less vertically challenged than I) off a dead tree that was precariously leaning over the trail.

Andy and I lined up about 3 rows back - this is a fast crowd and quickly came to a dead stop as the course narrowed to singletrack after only 10 feet of pavement. I chose to skip the first bridge and run through the mud which allowed me to pass about 5-6 runners. My goal was to go out at about last years pace and hope that I'm in better fitness and thus avoid bonking on the return half. The first 3 miles was about 5-10s/mile faster than last year and I had to constantly check my speed. This allowed Andy, Steve Wolfe and Chris Dunn to pass me. I hung on to Dunn and stayed within eyesight of Wolfe. Andy was gone. I got a little impatient when we hit the hills so I passed Dunn and the other runners in that group and felt great as we neared the turnaround. Andy was rocking the course and quite far ahead but Wolfe was reachable. I picked up the pace (slowly) and effectively caught (maybe 10s back?) Wolfe on the hills. When we returned back to the flat finish (3 miles left) I thought my only chance of beating Wolfe was picking it up here, passing him, and seeing if he would follow. I did pick up the pace but so did Wolfe but I hung on until the last little climb and descent. I passed Scott Spence on this small climb and hoped to catch Wolfe but he kicked in the turbo engines and took off downhill. Back on the flat river trail, with about 1.5 miles left, he just slowly drifted into the horizon. I had put some distance on Spence but could still hear him within striking distance. Indeed, Spence started to gain on me and with about 1 mile left he was in my wake and biding his time. I had nothing left to drop him and he passed me under I-93 with about 1/4 mile left (or less). I just didn't have the 2nd tank to race him. I did manage to negative split and finish in about 1:09:21 (18th overall, 5th old dude), which is almost a 4 minute PR from last year when I died.

I recognize that *everyone* is racing through their training but I'm pretty thrilled with this race given that I'm still on my ramp up phase from ski season and did an 8 X Bitch hill repeat Wednesday, a tempo run Thursday, and an easy 5 miler at RIT yesterday. I was also running on 4 1/2 hours sleep after driving 17 hours over the previous two days. All the trail monsters had strong races with Andy leading the charge in 1:07:xx and Emma taking 2nd overall! I'll get a medium-long run in tomorrow and then coast in to Boston next week for an "assisted training run".

Snowshoe racing, ski racing and running

Following my bad day at the Rangeley Loppet, I was a little depressed and decided to switch gears to running. I took a week off (mostly), skied the Carl Johnson on Saturday, snowshoe raced the Granite State Snowshoe Championship Sunday, and have focused on running this week, including a short, sweet hill climb Friday in Hope, ME. I skied the Sugarloaf Ski Marathon Saturday. So, lots to review!

Carl Johnson skiathon - good time trial that I wrote about in the previous post

Granite State Snowshoe Championship

As with the Blizzard, I entered the race with zero expectations, especially since I had skied a 3 hour time trial the day before (and on the same trail, at least for the first 5K). I started at a pretty moderate pace, which seemed to work at the Blizzard. Of course the Blizzard started with a steep climb while the first 5K of the GSSC was rolling hillets. Ian, Chuck, Jeremy and I were running together; Chris Dunn and Triffit were quickly out of site but we stayed within viewing distance of Steve Wolfe, so I'd say maybe 150-200 m behind him through about 3K. At this point, I picked up the pace a bit and I thought Chuck would go with me but he didn't; I didn't turn around so maybe he was right behind me. I passed a few runners that I didn't know and was slowly reeling in Wolfe. I basically caught him in the tunnel, which was the 1/2way point and marked the transition from the low rollers to the big climb. I thought about passing him before we got to the singletrack because passing on the single track would be tricky but I was reluctant because I was a little worried about bonking early. So I ran in Wolfe's wake for the first half of the climb; my singletrack technique could use some work and I fell at the start of the climb (yes on an uphill). About 1/2 way up the climb I asked to pass Wolfe and he kindly let me go. The climb felt great and I was feeling strong at the top. I did a quick turnaround and didn't see Wolfe or the other runner that I had passed just before the tunnel. I was now alone.

The long descent was a bit crazy because the probability of postholing was about 1-5%, which meant I'd be guaranteed of a few by the bottom. The postholes from the front runners were also intimidating. All I really thought about was falling and losing time so I'm glad I wasn't thinking about wrenching a knee like Ryan. About 1/2 way down I could see another runner quite far ahead but wasn't sure who it was. I found the descent long and boring and was ready to be done with it. I also figured I was running as fast as anyone could down this but I was wrong. At the bottom, as I turned into the woods, I turned around to see Wolfe had gained quite a bit on me. I didn't really assess how close he was but just seeing him meant close enough. I had actually recovered quite a bit on the descent and felt sharp on the rolling single track in the woods. I was gaining pretty quickly on the runner ahead of me and I figured it was Dunn. When I caught him, I mentioned that Wolfe was right on my tail hopig that Chris would pick up the pace. I ran in his wake for a short section but he kindly let me by and I maintained my previous pace, as I was still feeling quite good. I didn't turn around but I got the feeling that Wolfe was futher back than I thought. The woods trail dumped out onto a little trail next to Route 16 and I thought this was the end so I picked up the pace for a strong finish. Wooops. Unfortunately the race director (who coincidently was Chris Dunn) had other plans and sent us up some hellish powerline hill. I was mentally and now physically unprepared for this but having Dunn and Wolfe behind me was incentive to keep moving as fast as I could. After feeling great all race, now I was feeling aweful. I went through what seemed like an interminable series of ascents and descents and all I wanted to do was stop and walk, which I did for about 2s but again I had two big reasons to keep moving. I finally made it to the top of the final descent to the lodge and finish. I ended up 2nd master, 9th overall and not too far behind Ryan. I was dead, but happy with the results. Chuck, Jeremy, and Ian all came in soon after - we all had strong races. Acidotic racing threw a great awards party after and a late lunch at Moat with Jeremy, Ian, Emma, and Ryan helped to replenish lost calories.

I think I'll do more snowshoe running and racing next winter. It's a surprisingly low impact sport, and so compliments skiing nicely. I also like redlining my body - it's good preparation for shorter running races.

There are many really stunning photos of this race from Scott Mason, Joe Viger, Gianna Lindsey, and Great Glen Trails. I was the butt of a series of aural jokes about this one, which actually highlights my stunning balance NOT falling (you have to see the whole series). My favorite photo, of course, is this one here. As far as my, ah...heavy breathing, this started last year at Mother's Day 5K. I only do this when I'm redlining for many minutes, so typically a 5K but also some longer races as well (PT8K and this race). Maybe it's some kind of intense-exercise induced asthma. Does this give me an excuse to take albuterol before future races? I did like the response from one runner at GSSC that thought when I passed him at the 5K mark "yeh, I heard the breathing and thought, he's done, but then he just kept drifting further and further ahead" (I didn't even have my asmathic breathing at this point).

Hatchet Mountain Hill Climb - 1st hill climb of the season.

This is about 2 miles down the road from Cacky's parents house and it just opened up last summer but I hadn't run it before. I think some guy was going to build a house on the mountain and he built a wacky wicked steep driveway but then the permitting fell through and he abandoned it and there was a big drive to buy the property and create a community trail. So the 1st 3/4 of the trail is an abandoned split rock driveway and the last 1/4 is a narrow trail to the peak. The driveway part is wicked steep - I'm guessing 10-15% slope with 20% in sections. I was surprised that the peak is at 1100 feet so the total climb, from the Hope General Store (the hippest general store in Maine), was about 775 feet. I took the steep sections pretty hard but the overall run was short and sweet because I did have the Sugarloaf Ski Marathon the next morning!

Sugarloaf Ski Marathon

I'll keep this report short. This was my best 50K to date (although the actual distance was more like 44K). The course was 4 laps each of about 11K. It was a slightly different from last year and used part of the newly cut race course in the lower section. The temperature was perfect. The snow was mostly perfect. The major climb was packed well and actually very fast through all four laps. The wall on the lower part of the course sucked - it was chopped up transformed snow and the slope and chop made it hard to get a rhythm but I think I was climbing it better than those around me. The long descent in the top half was perfect and didn't slow at all in later laps. The sharp turns in the middle part of the course (from 4K-8K) were fast and rutted. On lap one I was skiing with fellow master blasters and took these all insanely fast for me and couldn't believe that I didn't go down on any of them. Or hit a tree. I was a little more cautious on my other three laps but still hit them pretty hard...with no falls (yes, my downhill turning training is paying off!). The new race course section had nice flow.

I managed almost perfectly even splits, which was a major goal of mine. My third lap was the slowest - I wanted to start picking up the speed but was reluctant because I didn't want to bonk and I instead skied it too slowly. I skied the lower section (the last 5K) of the last lap much faster and caught and passed three skiers and was catching up to another pack up three when the finish line got in the way. Given my final lap time I'm guessing I took the upper section climb in the first half a little too easy. Gotta figure out this pacing thing. I was a little tired from skiing hard the final 5K but think I could have skied harder on the other 40K. The problem is that finishing a race after bonking is really, really painful so maybe I'm too risk averse.

Splits: 1) 36:57.8, 2) 37:54.8, 3) 38:34.5, 4) 36:45.5

Official time: 2:30:08

Place 23/37 Men; 4/6 AG

The Colby skiers do a great job organizing this race and manning the feed stations and the course is fun so its a shame that more skiers don't have this marathon on the calendar. Lots of the fastest NE skiers were at Craftsbury this weekend but what about everyone else?

Carl Johnson Time Trial

I love ski racing! I still suck at it, though. Saturday was the third year in a row that I've skied 5K loops at Great Glen. Two years ago it was the Nordic 300, which was 5 hours (300 minutes) of skiing a 5K loop. That was my first introduction to severe dehydration. Last year and this, I skied the Carl Johnson Memorial Ski-a-thon to raise funds for ALS. The Carl Johnson is a how-many-laps-can-you-ski-in-3-hours skiathon. I was actually planning to ski the Bretton Woods marathon Saturday but the $75 price tag was too much and I opted for another year in the ski-a-thon. It was apparent that a bigger and more elite ski race was happening on the other side of Mt. Washington because at the start, I felt like I was crashing in on a private family reunion. There was a very athletic looking woman on classic skis and a few sub-driving-age folk who were darting around with impeccable skate technique. I guess this would be more of a time trial than a race (at least I hoped it wouldn't turn into a race - I'd hate to lose to a 12 year old girl). After a few photos of the wacky tights, the cannon fired, and I was off and in the lead (pheeeew, I got out in front of the kids!).

My strategy was to negative split, something I've never come close to doing in a ski marathon, so I took off at what I thought was a moderate race pace. I also figured I'd ski 8 x 21 minute laps, which is what I did last year (which was done in very positive splits). The first lap was probably my most eventful lap since I didn't know the course but was told to follow the orange discs with arrows. The disc went missing at one intersection so I stopped to ask a large group of recreational skiers if they knew the "nordic ski meister" course (the Tuesday night race course) and they brought out a map that had the course marked. Sure enough, I needed to take a right turn, which was confirmed by the athletic woman on classic skis that had now caught me. I took off again and stopped one more time because I made a turn without confirming with the orange discs. When I came into the start area, there were no water cups on the feed table and no one manning the table! In short order, the race director rushed over to pour me a cup, which was nice because that would have been hard with my hands inside of gloves inside of pole straps. I clicked "lap" on my watch, crossed the start/finish line, and looked at my watch: 21:06. Right on time except that I had easily 2 minutes of standing around during the lap, so either the pace was not moderate or I was skiing well.

My second lap was the 2nd most eventful lap. During one of the fast downhill sections I had to put on the brakes because the large group of recreational skiers that had helped me the previous lap were now skiing (but mostly talking) toward me. Then on the last little downhill I took my first gel but didn't want to throw the wrapper on the ground since this wasn't a real race. I just held on to the wrapper for the last 1.5K but dropped it twice, each time stopping to turn around and pick it up. I came into the feed station at the start/finish line to get some water to wash down the gel, clicked my watch: 19:58. OK, I thought, maybe I should just do 20 minute laps.

The problem with 20 minute laps is that this just gives you time to get a 9th in before the 3 hour curtain call. Which gave me something to think about for the next 5 laps...would I do a 9th lap? I continued to ski 20 minute (or just under) laps and these were pretty easy. I was practicing taking gels (not easy with gloves inside pole straps attached to poles) but my water stops at the start/finish line always were inefficient (as this wasn't a race, it wasn't set up to be efficient). On one downhill section I tried reaching into a lumbar pack pocket to grab some power/hammer/gu chews (cannot remember the brand) and struggled for about a minute (long after the downhill had run out) before giving up attempting to reach in a small pocket with gloved hands. Note to self - the chews are impossible with ski gloves, stick with gels.

The course itself was in excellent condition given the torrential rain the day before. The infamous Mt. Washington winds helped to dry the snow out and the temperature was about 30F all day instead of the predicted 40F. The steepest downhill turn quickly developed a deep rut that would have had me snowplowing two years ago and falling a couple of times last year. But my many hours working on downhill turns if finally paying off and the deep rut just added to the fun of a fast(ish) turn. My form felt sketchy on the first couple of laps but was feeling better and better with each lap (weird, huh?). At the end of the 7th lap, I had the nice race director help me with the bag of gu/hammer/cliff chews that I couldn't get myself earlier, and I drank some water, clicked lap on my watch, and noticed that I had a needed to average a little under 19:30s on each of the last two laps to get 9 laps in under 3 hours.

Not a problem. I skied the penultimate lap at a little faster pace and went through the start/finish without stopping for water or gu (the first time!). I forgot to press "lap" but I saw that I had about 20 minutes left so that must have been a 18:55 minute lap. I picked up the pace a little more on the final lap and about 1/2 way through caught and passed the athletic woman on classic skis. She was the last skier that I lapped and it took me 9 laps to do it. She said she wouldn't finish her 8th lap and I told her that she would (she did). I hammered the rutted turn and skied pretty hard home and finished the last lap in about 18:20. I felt great and could easily have gone on to do more laps. That was my fastest pace for a 50Kish distance race. I totally negative split, too, which I think was the key to the success. Each lap was about 5.3K so my totals were 47.8K in 2:58:26.

I won the most laps contest and felt a little guilty about taking it away from the 12 year old girl. I won a nice (woman's) headband that I donned at the Granite State Snowshoe race (report upcoming) as it totally matched my ibex striped woolies race shirt. Great Glen (and Snowman) put on some fabulous, low-key races - I hope they keep this one on the calendar for next year.

So I suck at ski racing

March is for ski racing and Team Blackstrap (neighbor John and I) kicked off the season with the Rangeley Loppet. Lots of other friends raced too. This is the fifth year I've skied and the fifth year I skied this race. I "toured" the first year because I was too chicken to register as a racer, then raced the 25K (2008), 50K (2009), 25K (2010), and now the 50K again. I was shamed into the 50K after doing the 25K last year but the reason I opted for the 25K last year is because ski coaching de-fits you. This year I attempted to coach and train for a 50K and felt pretty fit going in. We'll return to that thought in a minute. I work pretty hard on my skate technique and I was also feeling very good about all my gears and my downhill turns.

Rangeley hadn't received any of the rain/ice that southern Maine received in the past week so the conditions were a little bit of fresh snow on top of packed powder. I consider these conditions medium speed. The kind of crushed and groomed ice that we get at Pineland is what I consider fast. More importantly, the snow was soft enough that the climbs would get a little chopped sugar and the sharp turns would get very rutted, which would matter most on the 2nd lap.

I was placed in the first wave and by the time I got to the start I was at the end of the line in the first wave. No matter, I suck at ski racing so having all these folks in front of me would keep me from going out too fast. The first four miles feels flat and is a net downhill. There was an unpredicted high wind blowing down from Saddleback so drafting was a key strategery of mine that I've hadn't done well in previous years and I tried, largely unsuccesfully, to draft behind some Colby women and assorted old men that I had caught up too. The little down hills told me that my skis were slow so I had to work just to draft, which kinda misses the point.

Miles 4-12 include 3 big climbs of 220, 300, and 200 feet. The Colby women had dropped me on the downhill in between climbs 1 and 2 but I caught and passed 2 of them by the top of climb 2, which is the biggest and had a big wind in my face...or in the face of the master blaster I was drafting. I let the girls pass at the top of the descent because I thought they'd have faster skis. I've been really worried about my skis so I had them hotboxed this past week. This didn't do squat. The first part of the descent is less steep and I had to work hard to keep up with the women. Then we got to the dead tuck section and over about 3/4 mile I lost probably 200 meters. Uggg. My skis suck! And if I'm not gliding as fast downhill then I'm also not gliding as fast on the flats with each pole/skate push. Which all adds up to more work just to ski the same pace.

Miles 13-15.5 include the descent from the last climb and a flattish section in the bog. I had lost almost everyone in my group on the descent so I was now skiing alone. My legs were also very tired and I debated pulling over after the first lap and just taking a slow 25K time. But I didn't.

I skied alone the entire lap 2 and mostly thought about DNFing and heading back to eat chilli and chocolate chip cookies. The wind was ripping on the powerline trails (Saddleback actually closed all their lifts). My skis were even slower than the first lap. My legs were tired. And I was starting to feel the effects of dehydration, including cold hands (it was mid 30s temperature) because they had stopped sweating. I stopped to drink profusely at each feed station. I struggled to eat gels while skiing. It wasn't a repeat of the Great Glen 300 from two years ago but my body was semi-shutting down. For whatever reason, I pressed on and finished lap 2 about 14 minutes slower than lap one, which gave me a 3:14:11 overall time and 56/75 men.

My analysis: I felt very good about my technique and pretty good about my fitness going in but I'm not at all happy with my time. I did very little tempo or interval training and all but one of my long skis were punctuated with numerous stops because these were all done with friends. Real training requires skiing alone. Ultimately, I think I just suck at ski racing. On the positive side, this was my first race that I didn't fall and I was actually really comfortable hammering the rutted turns in the first lap (not so much lap 2 when I was wobbly from fatigue and dehydration).